DeltaG
免费的三维点云和网格数据处理软件
核心功能
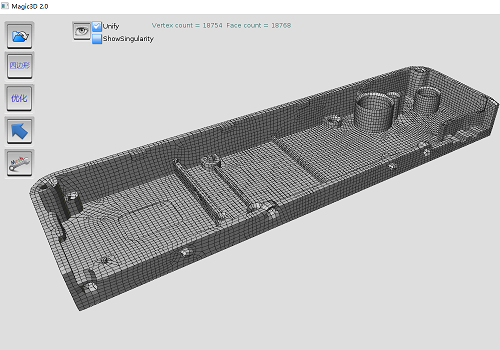
- 面向大场景的三角网格重建:支持大数据点云(上亿点);低内存消耗


创建和优化扫描点云的纹理网格
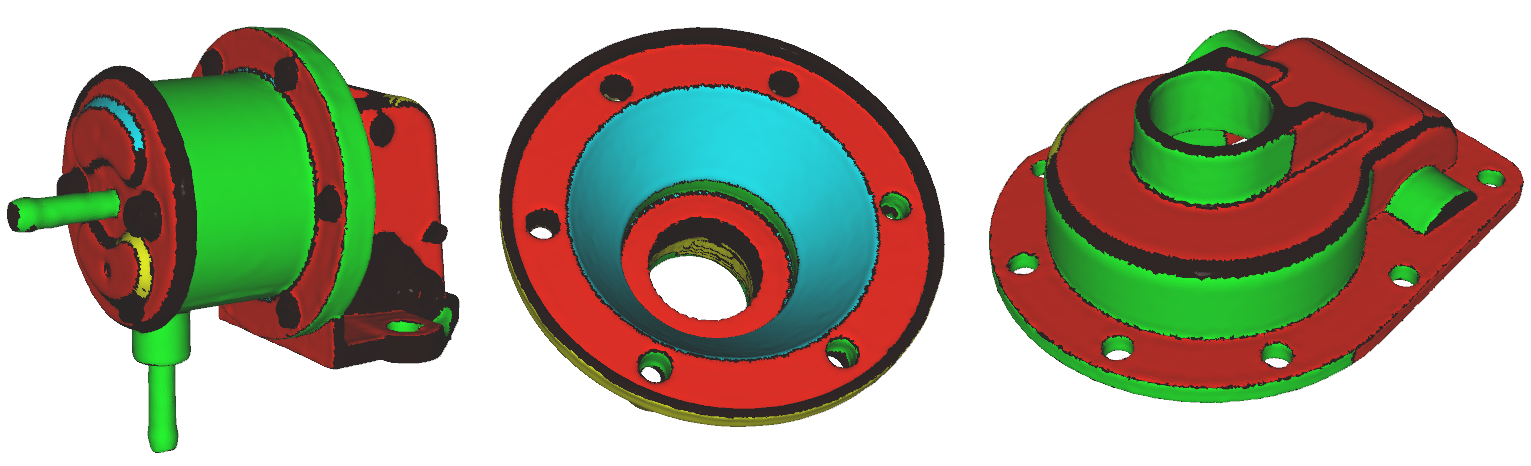
网格映射

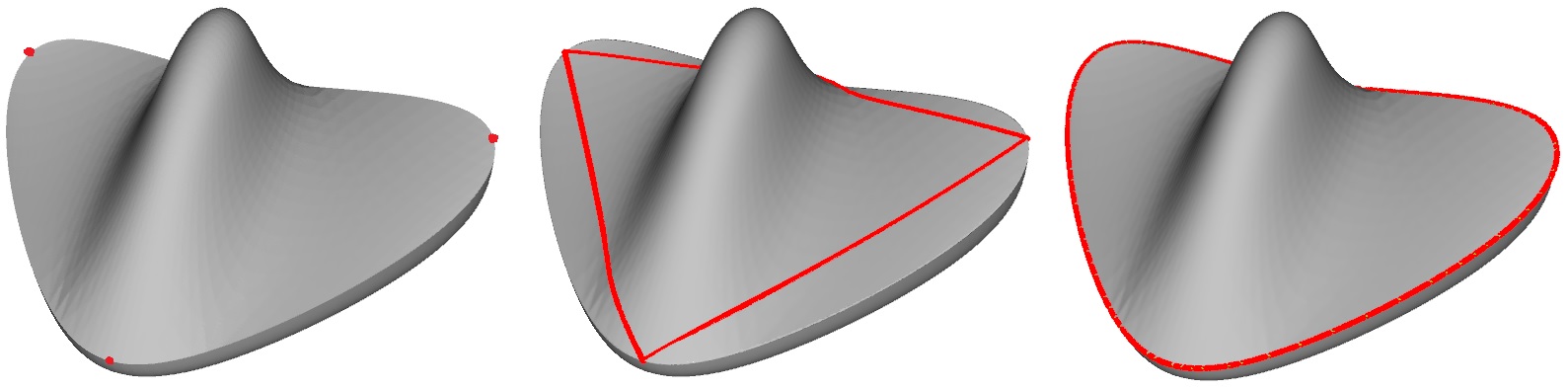
四边形网格创建与优化
- 四边形网格补洞
三角网格处理

如果您有任何疑问和建议,以及算法授权的相关问题,欢迎发email: