三维网格表示

网格有哪些数据结构

网格的数据结构其实就是一个图结构：点，边，面。可以是有向图，比如半边结构，也可以是无向图。在不同的软件或者开发包里，网格数据结构的实现都是有差异的。这种差异主要体现在网格连接关系的记录结构上，比如顶点是否记录邻域点，边，面信息，边是否记录邻域面信息等。记录的信息越多，查询的时候越方便，但是冗余的信息也越多，如果网格连接关系有变动，维护的信息也越多。另外，这些关系的建立也是需要开销的。所以，没有最好的数据结构，只有最适合当前算法的数据结构。

下面是一个例子：ITriMesh用于表达网格数据结构。网格算法都是基于ITriMesh接口来调用的，具体如下：

    class ITriMesh
    {
    public:
        ITriMesh(){}

        virtual Int GetVertexCount(void) const = 0;
        virtual Int GetTriangleCount(void) const = 0;

        virtual Vector3 GetVertexCoord(Int vid) const = 0;
        virtual void SetVertexCoord(Int vid, const Vector3& coord) = 0;
        virtual Vector3 GetVertexNormal(Int vid) const = 0;
        virtual void SetVertexNormal(Int vid, const Vector3& normal) = 0;

        virtual void GetTriangleVertexIds(Int fid, Int vertexIds[3]) const = 0;
        virtual void SetTriangleVertexIds(Int fid, Int vertexId0, Int vertexId1, Int vertexId2) = 0;
        virtual Vector3 GetTriangleNormal(Int fid) const = 0;
        virtual void SetTriangleNormal(Int fid, const Vector3& normal) = 0;
        virtual Int InsertTriangle(Int vertexId0, Int vertexId1, Int vertexId2) = 0;
        virtual Int InsertVertex(const Vector3& coord) = 0;
        
        virtual void SwapVertex(Int vertexId0, Int vertexId1) = 0; 
        virtual void PopbackVertices(Int popCount) = 0;
        virtual void SwapTriangles(Int fid0, Int fid1) =0;
        virtual void PopbackTriangles(Int popCount) = 0;

        virtual void UpdateNormal(void) = 0;
        virtual void Clear(void) = 0;

        virtual ~ITriMesh(){};
    };

ITriMesh是一个抽象类，不能直接使用。用户可以继承这个接口类，实现其成员函数。这样设计的一个好处是，用户无需改变自己已有的数据结构，只要实现了这个接口类，就可以调用所有关于网格的算法了。真正体现了即插即用的特点。比如用户已经有了一个三角网格类MyTriMeshData，则我们可以定义一个类MyTriMesh，并用它来调用各种网格算法：

    class MyTriMesh : public ITriMesh
    {
        MyTriMeshData* mData;
        MyTriMesh(MyTriMeshData* data) : mData(data) 
        {}
        virtual Int GetVertecCount() const 
        { 
            return mData->GetVertecCount(); 
        }
        virtual Vector3 GetVertexCoord(Int vid) const 
        { 
            return mData->GetVertexCoord(); 
        }
        virtual void SetVertexCoord(Int vid, const Vector3& coord) 
        { 
            mData->SetVertexCoord(vid, coord[0], coord[1], coord[2]); 
        }
        virtual Int InsertVertex(const Vector3& coord) 
        { 
            mData->InsertVertex(coord); 
            return insertVertexId; 
        }
        // 其它成员函数类似
    };

    MyTriMesh triMesh(myTriMeshData); // 用自己的三角网格数据初始化MyTriMesh
    ErrorCode res = ConsolidateMesh::LaplaceSmooth(triMesh, 0.2, 5, true); // 调用网格算法API来修改自己的网格数据
    res = ConsolidateMesh::MakeTriMeshManifold(triMesh);

---

半边结构好用吗

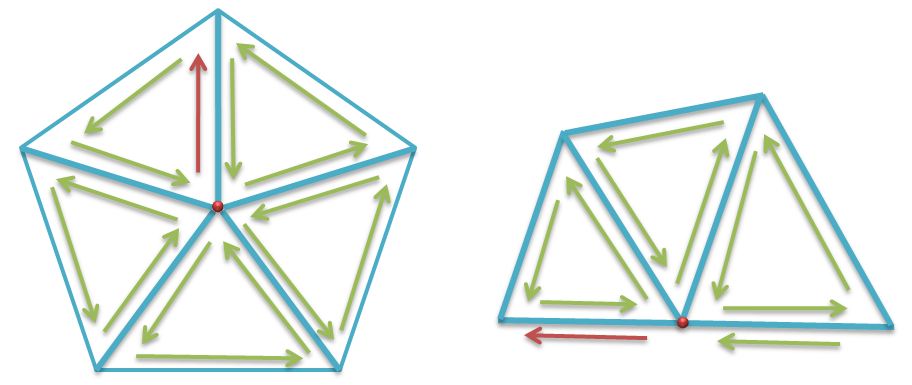
半边结构是网格数据结构的一种表达方式，它是一个有向图，把一条边表达为两个有向半边，如下图所示。它的优点在于网格信息的拾取非常方便，缺点是网格连接关系变动后，需要维护的信息也比较多。另外，半边结构表达的网格需要是流形结构，半边结构的构造也需要一定的时间开销。所以，一般场合我们都使用ITriMesh这类简单的网格表达方式。

---

网格有哪些属性

三角网格可以看作是一个图结构，由顶点，边和面（三角片）三个元素组成。网格的常见属性也由这三个元素的属性来表达。

---

网格顶点属性

顶点的几何属性通常可以表示为：

    struct VertexInfo
    {
        Vector3 mCoord;
        Vector3 mNormal;
    };

除此之外，它还有一些其它的属性：

邻域：邻顶点，邻边，邻面

流形：如果顶点的邻域是一个单连同区域，则这点为流形结构

colorId：对于一个彩色顶点网格，每个顶点有一个颜色值。如果这个网格是多个角度的数据拼接而成，则每个角度的网格片往往存在色差。colorId用于记录这个色差信息：同一个colorId的顶点，可以认为是颜色相容的，没有色差。colorId属性用于去除顶点色差的功能里。

---

网格边属性

边的几何属性一般由对应端点的几何属性来表达，所以它通常由拓扑属性来表达：

    struct EdgeInfo
    {
        int mVertexId[2];
        std::vector< int > mFaceIds;
    };

除此之外，它还有一些其它的属性：

边界边：如果它的邻接面为1，则为边界上的边

非流形边：如果它的邻接面个数 > 2，则为非流形边

---

网格面属性

面的常见表达方式为：

    struct TriangleInfo
    {
        Int mIndex[3];
        Vector3 mNormal;
    };

其中mIndex为三角片的顶点索引，mNormal为三角片的法线。三角片的属性其实用的并不多，它常见的属性是面点属性。所谓面点，即三角片的三个顶点。需要注意的是，面点和顶点的概念是不同的。下面是一些常见的面点属性：

面点法线：它和顶点法线是不一样的概念。比如特征尖锐的区域，可以设置面点法线为面法线；在光滑区域，设置面点法线为顶点法线。

纹理坐标：纹理坐标是一个典型的面点属性。严格来讲，顶点并没有纹理坐标的概念，只有三角形有纹理坐标的概念。网格UV展开到平面的时候，如果没有割缝产生，那么每个顶点在其相邻三角形内的纹理坐标都是一样的，故可简称为顶点的纹理坐标。如果有割缝产生，割缝处的顶点在不同三角形内的纹理坐标是不一样的。这时，顶点和纹理坐标是一对多的关系。其实，UV展开在UV域生成了一个二维网格，UV域的网格的顶点和原始网格的面点是一一对应的。所以，从这个角度来看SimplifyWithTextureCoords，它其实是对UV域的网格做了保持边界的QuadricSimplify操作。

点像对应：点像对应信息用于纹理贴图，它的含义是三角片的面点在图像中的对应。它的概念和纹理坐标是类似的，都是网格到二维区域的一个映射。点像对应信息在图像域也映射出了一个二维网格。和UV展开的区别在于，UV展开的二维域是唯一的，而点像对应的二维域（图像），有可能有多个（多张图片）。这导致某些三角片的面点可能对应于不同的图像域。对于这类三角片的纹理贴图，一般采用面点颜色插值。

注意：虽然点像对应是一个面点属性，Magic3D里的点像对应采用的却是顶点属性的表达方式，其主要原因是，网格的点像对应信息是从点云的点像对应映射过来的，所以可以认为每个顶点对应于一个像素。

---

网格法线计算

网格的法线可以分为三类：面法线，顶点法线，面点法线。

面法线：可以通过面的两条边做外积叉乘得到面法线

顶点法线：可以加权平均顶点的面邻域法线

面点法线：它代表了面里的顶点，而不是网格顶点，它与网格顶点是多对一的关系。比如正方体的一个角点，它有三个垂直的相邻面，面点法线可以取对应的面法线，而顶点法线则明显区别于这类面点法线。面点法线不是很常用。

看似简单的法线计算，要得到稳定的计算结果，需要考虑一些退化的情况。比如网格内有面退化的时候，该如何处理呢？