数值优化

有哪些数值优化的方法

在三维数据处理的算法里，绝大部分都可以归结为优化一个能量E = Edata + Eregular。Edata为数据项，一般表达了算法想达到的目的，比如变形算法里顶点的位置约束；Eregular为正则项，一般用于规范化解空间在可行的区域内，比如变形算法里的形状约束。有时候还有一些能量约束条件，包括等式和不等式约束。E通常是非线性函数。

线性问题一般可以直接求解线性方程组来解决。非线性问题，一般需要把问题线性化，然后用迭代的方法来逐次逼近解。比如E函数可以做Tylor展开，然后取前几项多项式来逼近E，然后求导求解。取到一次项，就是梯度下降法（最速下降法），取到二次项，就是牛顿法。

最速下降法

把能量函数做Tylor展开，然后取到1次项：

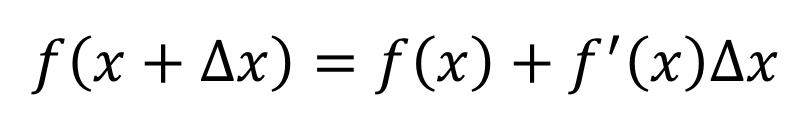
fomular

可以看出，f(x)沿梯度的负方向下降的最快，所以梯度下降法也叫最速下降法。有了下降方向和迭代步长a，则迭代过程可以表示为：

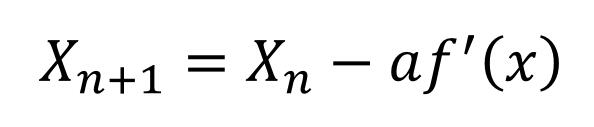
fomular

每次迭代过程中，需要求解迭代步长。这里没有标准的求解方法，需要根据具体应用来设计。最速下降法属于1阶收敛，收敛速度不快。

牛顿法

把能量函数做Tylor展开，然后取到2次项：

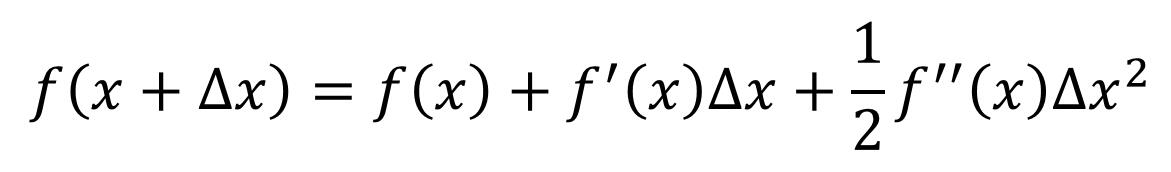
fomular

对这个等式进行求导，得到：

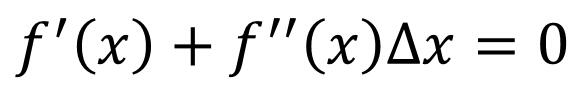
fomular

得出迭代公式：

fomular
  • 牛顿法的收敛速度很快，属于2阶收敛。从几何上看，2阶导数带有曲率信息，它可以帮助迭代过程更快的到达目的地；同样的，曲率信息对噪音也很敏感，有噪音的情况下，容易使得迭代过程发散掉。
  • 一般从一个初值开始，然后不断迭代。这个初值非常重要，它需要离真实的解很近，不然迭代过程很难收敛。甚至有些算法专门用于设计求解初值。
  • 有些函数的2阶导数（Hessian矩阵）逆很难求解，计算开销很大，或者根本就没有2阶导数。有些优化方法就用于近似的计算2阶导数（Hessian矩阵）的逆，比如拟牛顿法，常见的如BFGS，L-BFGS方法。